Puntos de silla
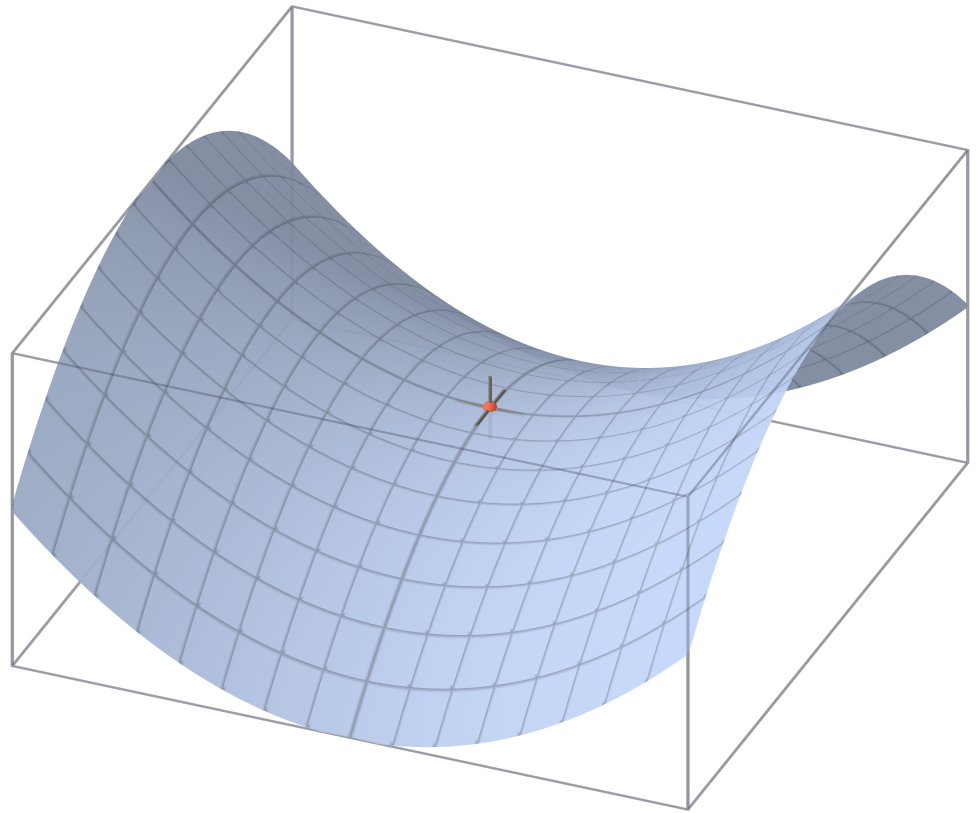
Los puntos de silla de una matriz son aquellos elementos de la matriz que cumplen que son menores o iguales que el resto de elementos de su fila y mayores o iguales que el resto de elementos de su columna, o al revés, mayores o iguales que el resto de elementos de su fila y menores o iguales que el resto de elementos de su columna.
Reciben este nombre por su similitud con una silla de montar a caballo; aunque el caso de la silla de montar es mucho más particular (los elementos a partir del punto de silla están ordenados).
Dada una matriz, queremos saber si tiene puntos de silla o no.
Entrada
La entrada está compuesta por diferentes casos de prueba. Cada caso comienza con una línea con dos enteros, el número F de filas y el número C de columnas de la matriz (entre 1 y 300). A continuación, aparecen F líneas cada una con C números enteros, que representan los valores de la matriz.
La entrada termina cuando el número de filas y columnas de un caso es 0. Este último caso no debe ser procesado.
Salida
Para cada caso de prueba se escribirá SI si la matriz tiene puntos de silla y NO en caso contrario.
Entrada de ejemplo
3 3 2 4 2 1 3 1 2 4 2 2 4 1 2 6 1 5 6 2 4 2 2 1 1 1 1 0 0
Salida de ejemplo
SI NO SI