Las luces en el río

Al alcalde no le parece suficiente tener un árbol de Navidad enorme iluminando toda la noche, y todos los edificios junto al río con luces para atraer turistas y curiosos incautos que aumenten la recaudación. También quiere aprovechar unos antiguos mástiles para banderas situados, con precisión suiza, cada 10 metros en la orilla para poner farolillos que den todavía más luz.
Para eso ha pedido al electricista del ayuntamiento que le haga las luces en su taller unidas con cables y me ha pedido a mi que las coloque. Como el alcalde, además, quería luces de colores, el electricista ha tenido la brillante idea de comprar varias parejas de bombillas, cada pareja de un color, y ha unido cada pareja con un cable independiente.
Pero el problema no es ese. El problema es que una pareja la ha unido con un cable de separación de 10 metros, de modo que sus dos luces se deben colocar en dos mástiles adyacentes. Las dos luces de otra pareja las ha unido con un cable de 20 metros, de modo que se deben colocar en dos mástiles dejando uno en medio. Y ha hecho lo mismo con el resto, y así tengo también una pareja distante 30 metros, otra 40, y así sucesivamente.
La gracia es que ahora soy yo quien tiene que lidiar con este desaguisado y conseguir poner un farolillo en cada mástil. El electricista asegura que se puede, porque tengo exactamente el mismo número de luces que de mástiles. Pero claro, tengo que buscar una colocación que sea viable dadas las longitudes fijas de los cables. Por si esto no fuera ya de por sí bastante difícil, el alcalde quiere que algunos mástiles tengan la luz de un color concreto, lo que me complica todavía más la tarea.
Entrada
Cada caso de prueba comienza con un número par indicando el número N de mástiles junto al río, todos situados en línea con 10 metros de distancia entre ellos. El electricista nos ha proporcionado N/2 parejas de farolillos, una uniendo sus dos luces con un cable de 10 metros, otra con un cable de 20 metros, y así sucesivamente hasta 10×N/2 metros.
A continuación aparecen N números separados por espacio, uno por cada mástil del río, en el mismo orden. Cada número representa la exigencia del alcalde para ese mástil. Un 0 indica que el alcalde no ha impuesto ningún color a la luz de ese mástil. Un número K indica que en esa posición tengo que poner el color asociado a la pareja de luces que están unidas por un cable de longitud 10×K.
Se garantiza que 2 ≤ N ≤ 32, que el resto de números están entre 0 y N y que como mucho hay 10 ceros. El alcalde, además de tener ideas peregrinas, hace a veces exigencias que son imposibles de cumplir desde el principio.
Salida
Por cada caso de prueba el programa escribirá de cuántas formas se pueden colocar los farolillos en los mástiles cumpliendo las restricciones del alcalde y el electricista.
Entrada de ejemplo
8 0 0 0 0 4 0 0 0 8 0 2 0 0 4 0 0 0 8 0 2 2 0 4 0 0 0
Salida de ejemplo
2 1 0
Notas
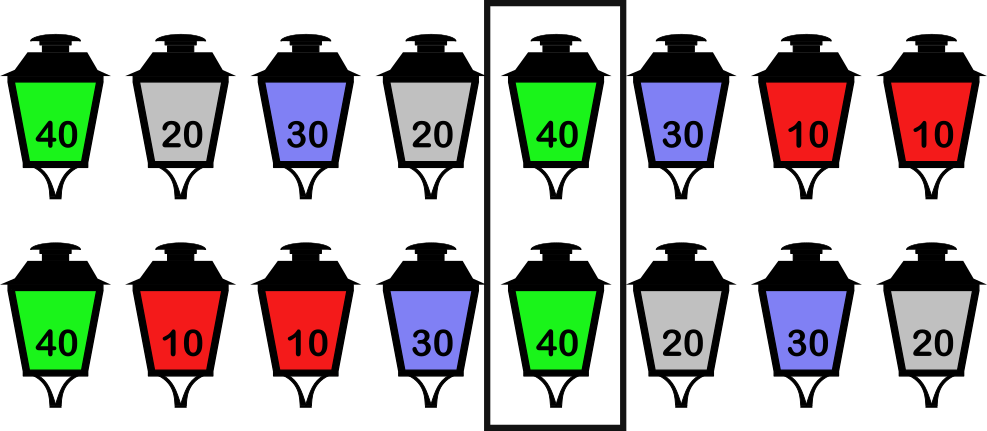
Si hay 8 mástiles tendremos 4 parejas de colores, a distancias 10, 20, 30 y 40 metros. Si el quinto mástil empezando por la izquierda tiene que tener el color asociado a la pareja que está distante 40 metros (debe tener 3 mástiles entre sus farolillos) hay exactamente dos configuraciones posibles: