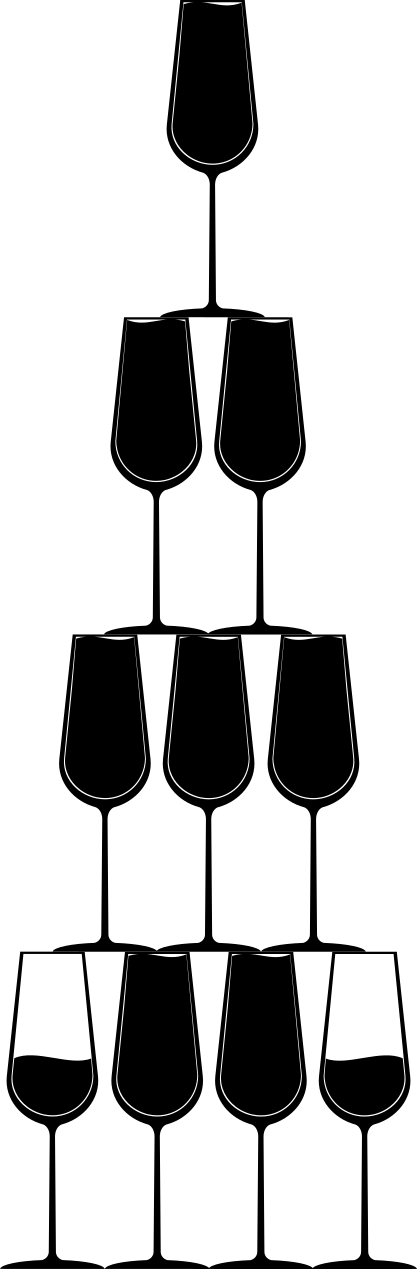
Torres de copas

En celebraciones muy especiales en las que los anfitriones optan al nivel máximo de sofisticación no falta la famosa construcción de copas en la que sobre una base de copas situada en una mesa se coloca otra capa, que a su vez tiene otra capa encima y así las veces que sean necesarias hasta que al final, arriba del todo, una única copa culmina la construcción.
Entonces, en el momento seleccionado (por ejemplo al terminar la comida en una boda) los anfitriones dejan caer su bebida espumosa favorita en la copa superior que, al llenarse, rebosa y el líquido pasa entonces a llenar las copas de la capa inmediatamente debajo. Cuando estas van llenándose, el líquido pasa a llenar la tercera capa y así sucesivamente.
Aunque las torres suelen tener profundidad, por simplicidad consideraremos una torre triangular en la que la copa de la cúspide está apoyada únicamente en dos copas de forma que cuando rebosa, el líquido sobrante se reparte íntegramente entre ambas de manera ecuánime sin desperdiciar nada. A su vez ese segundo nivel de la torre está apoyado en un tercer nivel con tres copas y así sucesivamente. Al final, el excedente de cada copa se reparte entre las dos que tiene debajo y, al mismo tiempo, cada copa, salvo en los extremos, recibe líquido de las dos que tiene encima.
Con esta estructura triangular lo normal es que el número de copas de la construcción sea superior al número total de invitados. Por ejemplo, si tenemos cuatro invitados haremos una construcción con tres niveles y seis copas. Si queremos ahorrar bebida, dejaremos de echar líquido en la copa superior cuando tengamos cuatro copas completamente llenas, aunque haya dos que aún estén a medias.
Lo que queremos es saber, dada una construcción triangular de copas, cuántas botellas necesitaremos para conseguir llenar al menos tantas como invitados tengamos. En nuestra torre de copas, además, tenemos copas de distintas capacidades: las que ocupan capas con un número impar de copas (la capa superior, la tercera, quinta, etc.) tienen una capacidad y las de las capas pares otra.
Entrada
La entrada está formada por distintos casos de prueba, cada uno en una línea.
El primer número indica la cantidad de niveles que tiene la torre de copas (entre 1 y 20). A continuación vienen las capacidades de las copas de los niveles impares y de los niveles pares (ambas entre 1 y 16). El cuarto número indica la cantidad de líquido que entra en una botella (entre 1 y 32) y por último aparece el número total de invitados a la fiesta. Se garantiza que hay al menos tantas copas en la construcción como invitados.
Salida
Por cada caso de prueba se escribirá cuántas botellas se necesitan como mínimo para llenar por completo copas suficientes para todos los invitados que hayan acudido.
Ten en cuenta que al final del proceso es posible que alguna otra copa haya quedado a medio llenar. En una celebración tan sofisticada esas copas se deshechan; a los invitados se les dan únicamente copas completamente llenas.
Entrada de ejemplo
3 1 2 1 1 3 1 2 1 3 3 1 2 2 3 3 1 2 1 5 4 1 1 1 8
Salida de ejemplo
1 5 3 9 9
Notas
La figura siguiente muestra el resultado del último ejemplo. Las dos copas de los extremos del nivel inferior están a un cuarto de su capacidad. El contenido de la mitad de la última botella usada termina sobre la mesa.