El campus de Jussieu

En la orilla izquierda del Sena, en el corazón de París, se encuentra el campus de Jussieu. Lo comparten varias instituciones, entre otras la que fue la Universidad de París VI Pierre et Marie Curie, hoy refundada en la Universidad de la Sorbona.
El campus está compuesto por una rejilla de edificios de 6 plantas con soportales peatonales. En las intersecciones se encuentran las escaleras y ascensores para acceder a los hasta 4 edificios que conectan.
Para facilitar la orientación, las intersecciones están numeradas de acuerdo a su posición en la rejilla con dos números indicando la "columna" y la "fila" en la que están. Como el número de columnas y filas es menor que 10, los dos números se fusionan en uno solo, de dos dígitos. Así la intersección 23 se refiere a la situada en la "columna" 2, "fila" 3. Los edificios, a su vez, se identifican por la pareja de intersecciones que conectan.
Pese a la regularidad de su diseño, no en todos los lugares donde debería haber una intersección hay un acceso con escaleras y ascensor, lo que reduce el número de edificios del complejo.
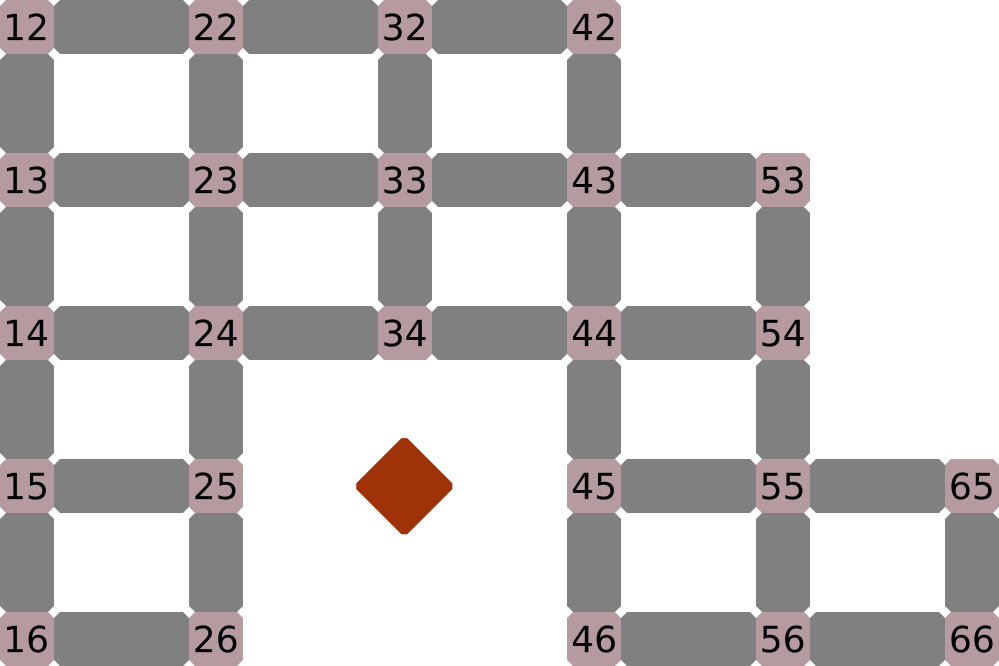
Entrada
Cada caso de prueba comienza con dos números 2 ≤ c, f ≤ 100.000 indicando, respectivamente, el número de columnas y filas de edificios en la rejilla. A continuación, en la misma línea, aparece un tercer número 0 ≤ h < min(250.000, c×f) indicando el número de huecos en las intersecciones, es decir en cuántas intersecciones falta el acceso.
A continuación aparecen h pares de números indicando cada uno el número de columna (entre 1 y c) y número de fila (entre 1 y f) de una intersección ausente. Como el tamaño de la rejilla puede ser grande, ambos números aparecen separados por espacio, en contra de lo que ocurre en la numeración del campus de Jussieu. Se garantiza que cada intersección ausente aparece únicamente una vez.
La entrada termina con tres ceros.
Salida
Por cada caso de prueba el programa escribirá el número de edificios que tiene la rejilla del campus. Para que un edificio se construya deben existir las dos intersecciones que conecta. En particular, puede ocurrir que exista una intersección sin edificios adyacentes porque faltan las cuatro intersecciones contiguas.
Entrada de ejemplo
2 2 0 2 2 2 2 1 1 2 6 6 12 1 1 2 1 3 1 4 1 5 1 6 1 5 2 6 2 6 3 6 4 3 5 3 6 0 0 0
Salida de ejemplo
4 0 35