Suma de árboles
Si tenemos dos árboles binarios, podemos sumarlos. La idea de la suma consiste en poner un árbol encima del otro solapándolos, de forma que las raíces de ambos queden una encima de otra, sus hijos izquierdos también, etc. El árbol final tiene por tanto la estructura combinada de ambos árboles y, en los casos donde dos nodos coincidían, el valor del nodo final es la suma del contenido de los dos nodos originales.
Como ejemplo, aquí aparecen dos árboles y su árbol suma:
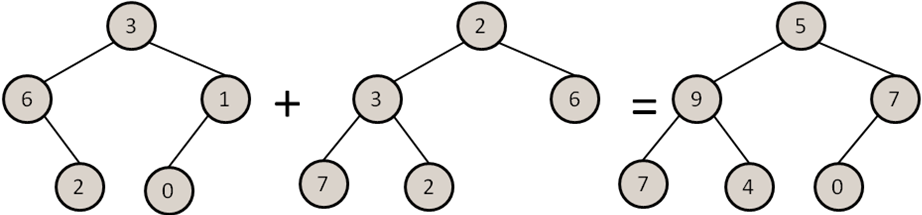
Entrada
Cada caso de prueba consiste en dos árboles de enteros. Cada uno de ellos comienza con el contenido de su raíz (un entero no negativo), al que le sigue la descripción del hijo izquierdo y después la del hijo derecho. El número -1 indica la ausencia de hijo o lo que es lo mismo, el árbol vacío.
Los casos de prueba terminarán cuando ambos árboles sean vacíos. Ese caso de prueba no generará ninguna salida.
Salida
Para cada caso de prueba se escribirá una línea en la que aparecerá la descripción del árbol suma siguiendo el mismo formato que en la entrada (ten en cuenta que al final del último número no debe aparecer un espacio).
Se garantiza que el árbol resultado no tendrá nunca más de 10.000 nodos, y que cada uno de ellos no tendrá un número mayor que 109.
Entrada de ejemplo
1 -1 -1 2 -1 -1 1 2 -1 -1 3 -1 -1 5 -1 6 -1 -1 -1 -1
Salida de ejemplo
3 -1 -1 6 2 -1 -1 9 -1 -1