La mezcla de Juancar

Juancar Nariz es un experto mago capaz de hacer trucos de cartas increíbles, que le han llevado a actuar a lo largo y ancho de todo el mundo. Tiene una soltura envidiable manejando los naipes y es capaz de hablar mirando al público mientras mezcla un mazo de cartas de forma que queden colocadas tal y como las necesita para su próximo efecto.

Uno de sus métodos de mezcla, que ejecuta a velocidad pasmosa, comienza invirtiendo el orden de todo el mazo, de modo que las cartas que estaban abajo pasen a estar arriba en sentido opuesto (paso 1 en el siguiente dibujo). Si tiene al menos cuatro cartas, a continuación divide la pila en dos grupos exactamente iguales (paso 2) y los entrelaza al estilo americano, poniendo primero la carta inferior del lado izquierdo, luego la inferior del lado derecho, luego la segunda del izquierdo, y así sucesivamente (paso 3).

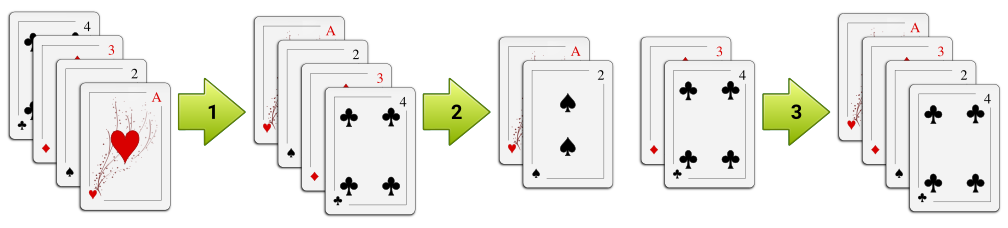
Tiene tan entrenado el proceso que nunca comete el más mínimo error y ante una configuración de partida sabe el orden final exacto que conseguirá. Cuando tiene la sensación de que el público también lo conoce, complica más el proceso para despistar. Tras dividir el mazo en dos mitades cuando tiene al menos 4 cartas, antes de entrelazar las cartas aplica el mismo procedimiento de mezcla de manera separada y completamente a cada una de las dos mitades, lo que puede provocar que también se aplique a las dos mitades de cada mitad, etcétera.

Entrada

Salida

Entrada de ejemplo

2
1 2
2
3 4
4
4 3 2 1
0

Salida de ejemplo

2 1
4 3
2 4 1 3